对于神经网络，我们要做的是降低网络的弹性，使得它专注于当前任务，因此我们构建了各种架构。自注意力模型希望找出一段seq中的输入值的相关性，因此我们手动构建了一个方便机器快速计算出相关性的模型。

Self-attention

  • Dot-product：两个向量分别乘上一个矩阵后得到的向量(query, key)做Inner-Product得到attention score(关联性)α\alpha

q1=Wqa1k1=Wka1α1,1=q1⋅k1q^1 = W^qa^1\\ k^1 = W^ka^1\\ \alpha_{1,1} = q^1 \cdot k^1

  • 对得到的关联性进行归一化处理得到attention score矩阵
  • seq中每个向量乘上一个矩阵后得到的新向量v，乘上attention score之和（有点类似于加权，权重为attention score）等于向量b。

b1=∑iα1,i′vib^1=\sum_i \alpha^{\prime}_{1,i}v^i

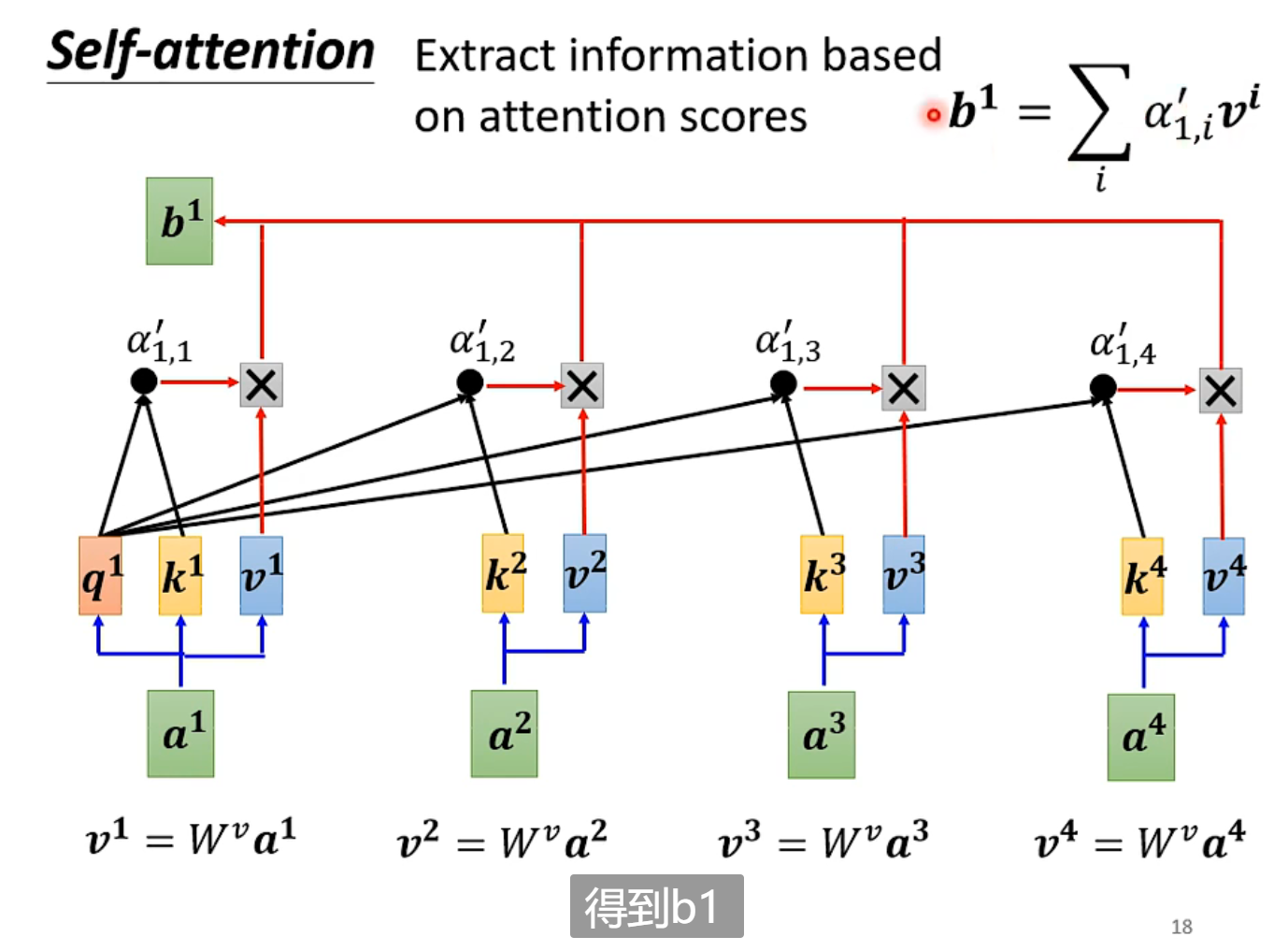
image-20221117193029514

谁的attention score α\alpha更大，谁(v)对bb的影响更大

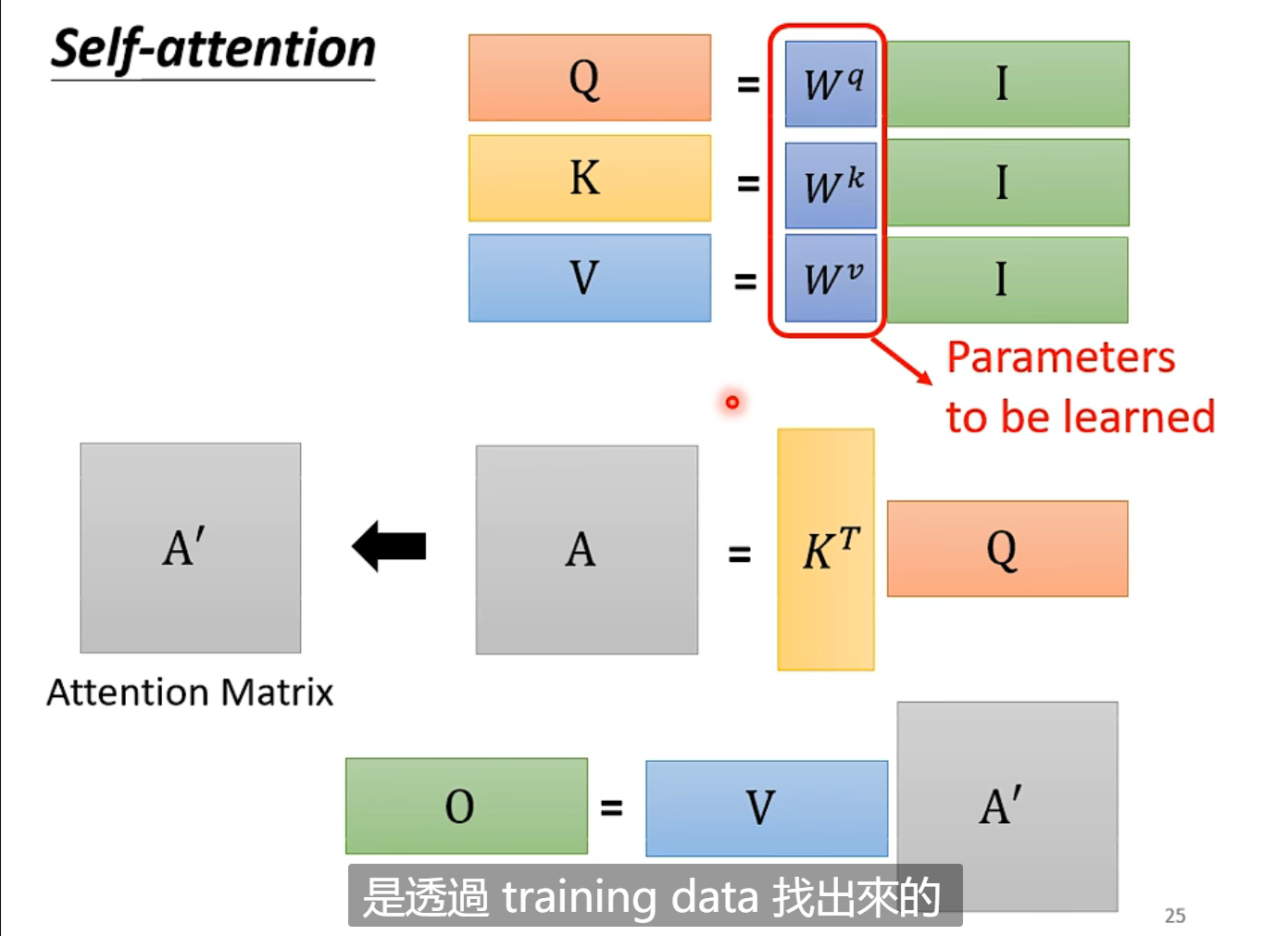
从矩阵运算角度描述Self-attention

I:input matrixA:attention scoreQ=WqIK=WkIV=WvIA=KTQB=VA′I:input\ matrix\\ A:attention\ score\\ Q=W^qI\\ K=W^kI\\ V=W^vI\\ A=K^TQ\\ B=VA^{\prime}

  • 输入矩阵II分别乘以Wq,Wk,WvW^q, W^k, W^v三个矩阵得到Q,K,VQ, K, V

  • A=KTQA=K^T Q ，经过归一化处理后得到自注意力矩阵A′=softmax(KTQdk)A^{\prime} = softmax(\frac{K^T Q}{\sqrt{d_k}})

  • 输出矩阵O=VA′O=VA^{\prime}

image-20221117112430851

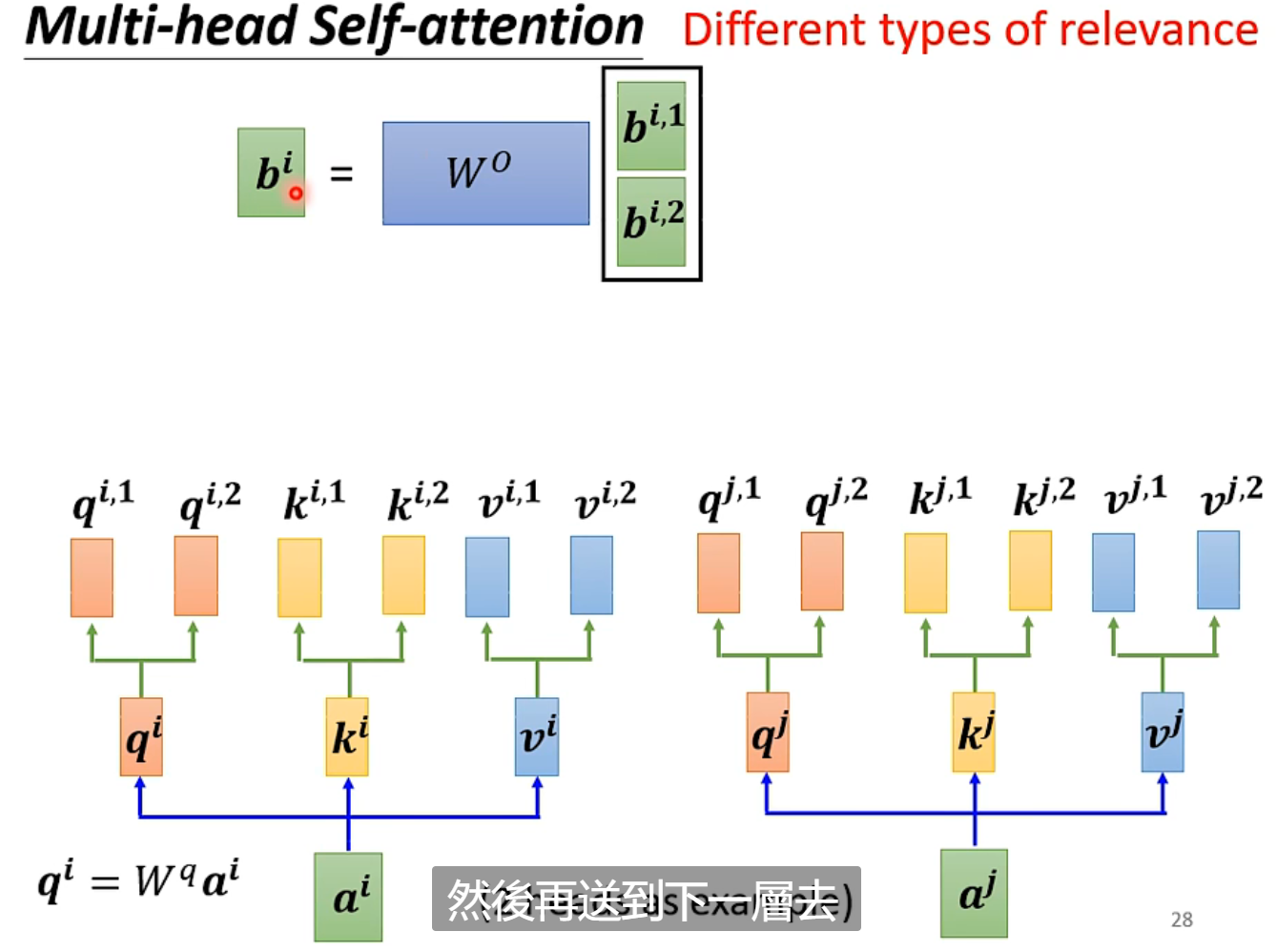
Multi-head Self-attention

一次Self-attention的query，key都相当于询问一次相关性。在实际应用中，对于相关性往往不止一种定义。所以，我们需要不同的q，去问不同的k，得到v之间不同维度的相关性。

在实际操作中，对得到的qi,ki,viq^i,k^i,v^i，分别做不同的映射得到qi,1,qi,2,...,ki,1,ki,2,...,vi,1,vi,2,...q^{i,1},q^{i,2},...,k^{i,1},k^{i,2},...,v^{i,1},v^{i,2},...，最后把得到的bi,1,bi,2,...b^{i,1},b^{i,2},...计算得到bib^i

image-20221118213000253

Positional Encoding

对于当前Self-attention，缺少关于位置的信息。需要在输入中添加位置Embedding，否则Transformer就是一个词袋模型了。

为每一个位置设定一个positional vector eie^i，表示位置信息。加到原向量aia^i上。

Truncated Self-attention

当面对较长的sequence时，会导致Attention Matrix过大，所以有时只需要关注小范围就可以识别当前vector的讯息。

Self-attention vs CNN

Self-attention考虑了全局的讯息，而CNN只考虑receptive field内的信息

因此，CNN可以看作是简化版的Self-attention，Self-attention也可以看作是复杂的CNN，相当于receptive field也是机器自己学到的。

由此，从模型的弹性角度来看，更flexible的模型Self-attention，更容易overfitting，需要更多的data。

Self-attention vs RNN

和RNN相比，更适合处理和当前vector距离较远的vector，以及可以并行运算在运算速度上更快。

如何减少Self-attention的运算量，做到又快又好？